PID에 wrapper로 올릴 수 있는 meta-controller를 개발했는데 논문 한번 봐주실 분 있나요?

논문은 techRxiv에 있습니다(DOI: 10.36227/techrxiv.176281113.30584908/v2)
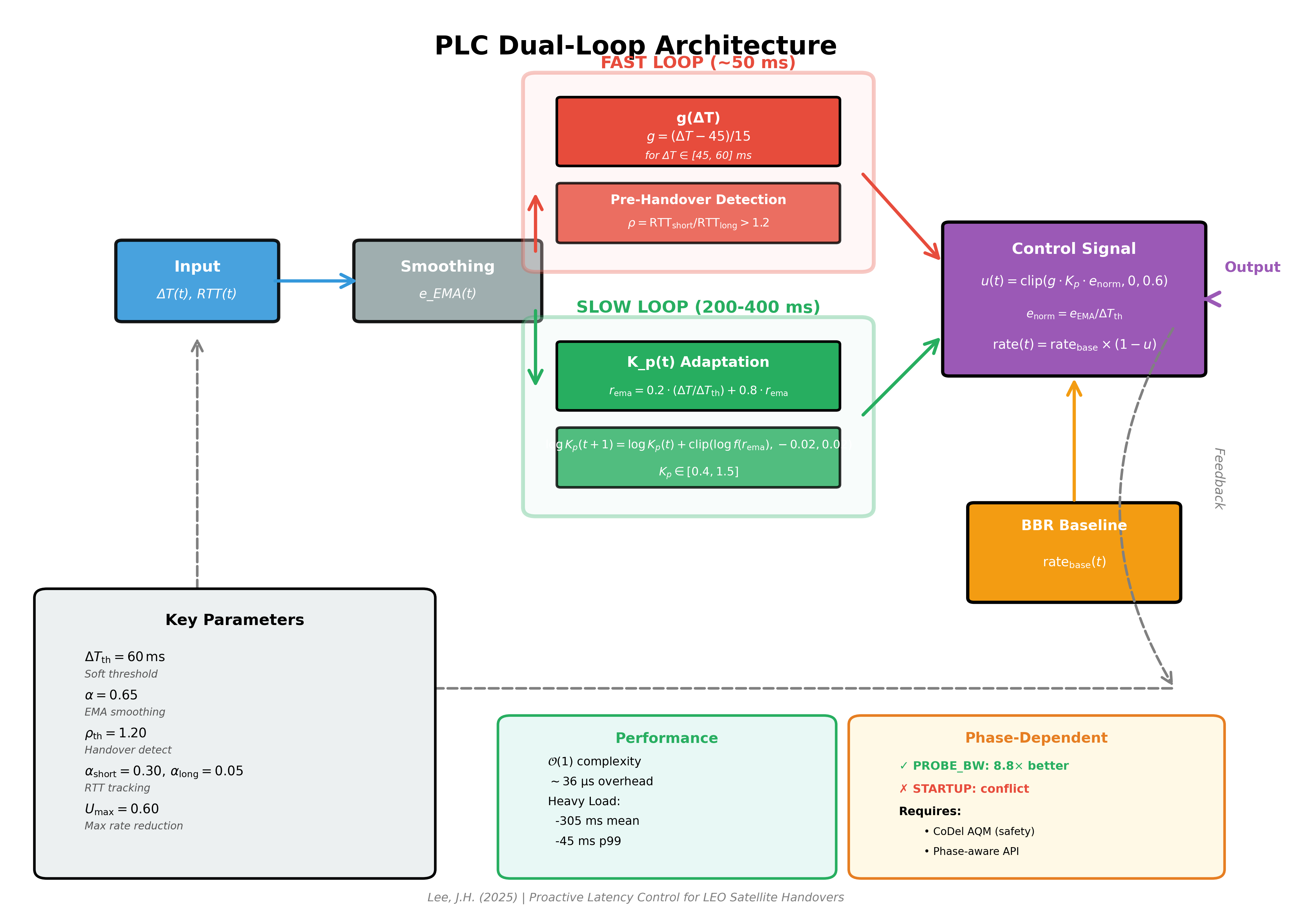
https://www.techrxiv.org/users/985845/articles/1357489-proactive-latency-control-robust-dual-loop-adaptation-for-predictably-uncertain-leo-networks

Smith Predictor의 예측성, Gain scheduling의 적응성, Anti-windup의 안정성을 지향하되, 이를 복잡한 모델링 없이 단순 피드백 루프로 구현함으로써 기존 제어기(PID) 위에 가볍게 얹을 수 있는 Wrapper 형태이고요, 원래는 전송제어프로토콜인 BBR의 rate를 조절해서 저궤도 위성통신 조건에서 latency를 줄여보려고 만든건데 PID 위에도 올릴 수 있습니다.

Kₚ를 log-domain에서 작은 스텝으로 제한된 multiplicative update로 조정함으로써 모델 없이도 bounded stability를 유지하며
환경 변화에 따라 천천히 gain을 조절하는 방식입니다.

주요특징은 아래와 같아요
bounded-log adaptive gain
EMA fading memory
time-scale separated dual-loop
Lyapunov-stable multiplicative update
O(1) complexity

전력망에 쓰게 되면 아래와 같은 방식이지 않을까 싶습니다.

1. 기술 개요 (PLC → 전력망 그리드 적용)
위성통신 지연제어 기술인 PLC(Proactive Latency Control)을 ESS 주파수 제어에 적용: log(K_p) ← log(K_p) + clip(log(f_r), -0.02, 0.02)
- r_ema = 현재 주파수 / 목표 주파수 (60Hz)
- f(r) = 1.0 / (1 + θ×max(0, r-1)) 자동 감쇠
- 결과: 주파수 변동 ±0.2Hz → ±0.05Hz 안정화 예상

2. 기존 방식 한계 및 개선점
기존 PID: 3파라미터 튜닝, 진동 문제, 부하변화 취약
Clip Rule: 단일 K_p 자동 적응, 로그 도메인 BIBO 안정성, r_ema 기반 실시간 적응

3. 수학적 안정성 증명 (Lyapunov)
Lyapunov 함수: V = e² + (K_p - K_p*)²
제약: |K_p(t+1)/K_p(t)| ≤ 1.0202
증명: V(t+1) ≤ V(t) → 수렴 보장

4. 코드 예시 (18줄 Python)
for each 100ms cycle:
# (1) 측정
freq = measure_frequency() # Hz

# (2) 비율 계산
r_instant = (60.0 / freq) * sensitivity
r_ema = 0.20 * r_instant + 0.80 * r_ema

# (3) 감쇠 함수
f_r = 1.0 / (1.0 + max(0, r_ema - 1.0))

# (4) Clip Rule
log_K = log(K_ess)
log_K = log_K + clip(log(f_r), -0.02, 0.02)
K_ess = clip(exp(log_K), K_min, K_max)

# (5) ESS 출력
P_ess = K_ess * (60.0 - freq) * P_rated
apply_power(P_ess)